这是一皆八年龄数学几何题:难度特别大!解题重要:怎样作适合的支持线?怎样构造全等三角形?好多孩子毫无眉目、无奈只有留住空缺!
如图一,
图一
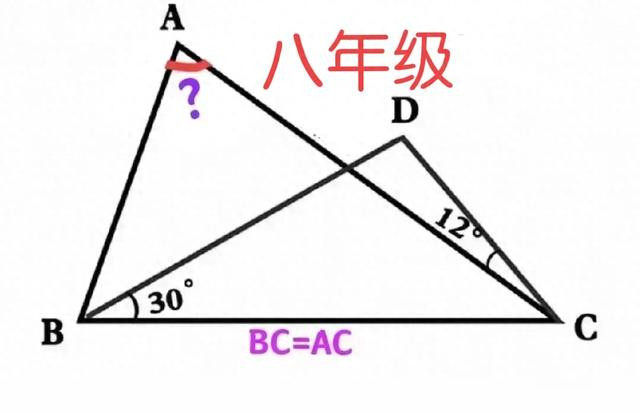
在三角形ABC中,AC=BC,点D在AC中垂线上,∠CBD=30°,∠ACD=12°,求∠A=?
分析:
30°角每每用于构造直角三角形或等边三角形!故可研讨从∠CBD=30°脱手!并抽象欺诈“AC=BC”及“点D在AC中垂线上”这两个条目!
“点D在AC中垂线上”可推出AD=CD,荟萃“AC=BC”,可向用于“解说三角形全等”这个标的研讨!
—————————
教唆一:构造一内角为30°的直角三角形+三角形全等!
①过点C作BD延迟线的垂线CE,如图二

图二
则∠BCE=60°,CE=BC/2=AC/2。
②过点D作AC的垂线DF,由点D在AC中垂线上可知,CF=AF=AC/2=CE,故△CDE≌△CDF,ag百家乐三路实战从而∠DCE=∠DCA=12°,∠ACE=24°,∠ACB=60°-24°=36°。
③∠BAC=∠ABC=(180°-∠ACB)÷2=72°。
教唆二:构造等边三角形+三角形全等!
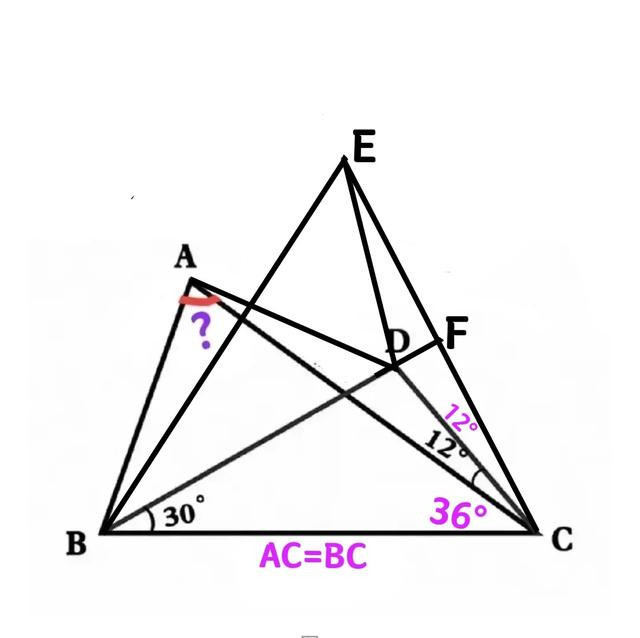
①以BC为边进取作一等边三角形BCE,延迟BD与CE相交于点F,如图三
图三
则BF垂直CE(BF三线合一,即BF为CE上的中线和垂直瓜分线、∠CBE的角瓜分线),故CD=DE。
②由D在AC中垂线上可知AD=CD,再有AC=BC=CE,故△ACD≌△ECD,从而∠ECDC=∠ACD=12°,从而∠FCA=24°,∠ACB=36°。
———————————
友友们ag百家乐老板,奈何看?宽宥留言共享!
