在探索四维空间多出的维度之前，让咱们先梳理一下从低维度到三维空间的办法。

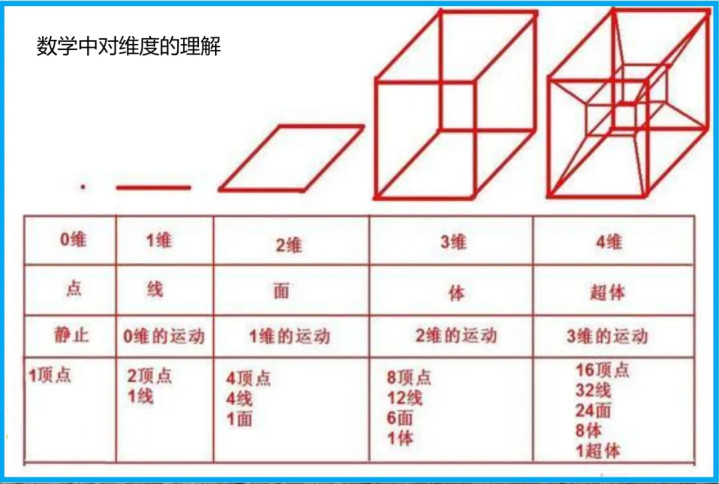
零维是一个无穷小的点，小到莫得直径、长宽高，不占据任何履行空间，如引力质点或奇点，是一切维度的肇始 。从这个点开赴，当大皆个零维点沿一个地方罗列，便变成了一维空间，它唯独长度，莫得粗细，像一条莫得宽度和高度的逸想直线，仅能向两头无穷延展，比如数轴上的线，线上每个点皆不错用一个实数来闪现位置，解放度为 1。

当一维的线在另一个方朝上延展，就组成了二维空间，它有长和宽两个维度，变成了一个平面，领有面积却莫得厚度，像一张莫得厚度的纸。在二维平面中，每个点皆不错用一双实数（x，y）来笃定位置，比如舆图上的地点，通过经度和纬度这两个坐标就能找到其位置，解放度为 2。

接着，二维平面在垂直于本人的方朝上持续堆叠，大皆个二维平面的换取产生了三维空间，也即是咱们往常生存所处的寰宇，它具有长、宽、高三个维度，能容纳立体的物体，领有体积。咱们所处的房间，房间里每个点的位置皆不错用三个坐标（x，y，z）来闪现，比如笃定天花板上某盏灯的位置，就需要知谈它在长、宽、高三个方朝上相干于房间某个基准点的距离 ，解放度为 3。

咱们所生存的三维空间，是一个由长、宽、高三个维度相互交汇构建而成的立体寰宇 ，这三个维度相互垂直，共同笃定了物体在空间中的位置。在这个空间里，大到寰宇中的天体，如行星、恒星，它们有着雄伟的体积和复杂的结构，占据着广泛的三维空间；小到微不雅寰宇的基本粒子，天然圭臬极小，但还是存在于三维空间的框架内。

往常生存中的物体，比如咱们居住的房屋，从长度上看，它有一定的进深；从宽度上，有不同的开间；从高度上，有楼层的高度。房屋的每一个房间、每一件产物，皆在这个三维体系中有其特定的位置和体积。再比如咱们往常使用的杯子，它有高度，有杯口的直径（体现宽度），还有从杯口到杯底的长度，这些维度共同组成了杯子的三维形态，让它能够盛装液体 。

在三维空间中，物体的畅通也顺从着特定的物理章程，举例牛顿畅通定律。当咱们投掷一个篮球时，篮球会在重力、空气阻力等外力的作用下，沿着一个复杂的三维轨迹畅通，其畅通轨迹不错通过在三个维度方朝上的速率、加快度和时辰等参数来精准神情。三维空间中的物理章程，如引力、电磁力等，它们的作用结束也皆依赖于物体在长、宽、高三个维度上的位置和相互相干 。

那么，四维空间呢？

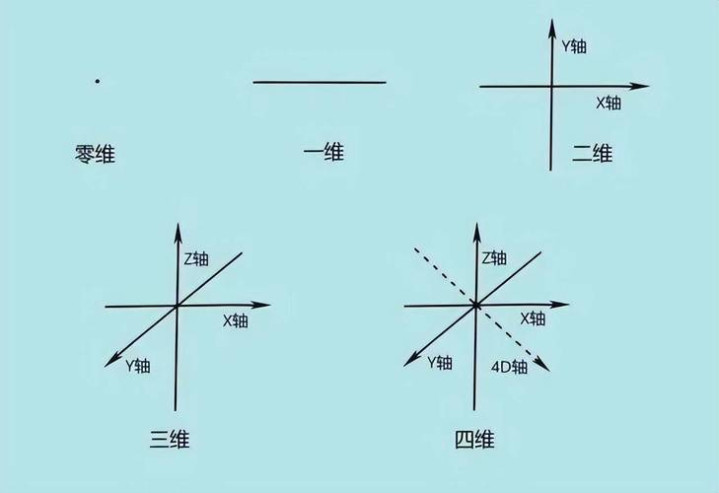
在数学限制，四维空间是一个在三维空间基础上增多了一个维度的办法。浅近来说，它是由四条相互垂直的线所笃定的空间，每个点皆不错用四个坐标（x，y，z，w）来闪现 。在咱们往常的三维空间中，一个立方体由三条相互垂直的边组成，笃定一个偏抓需要三个坐标。而在四维空间里，与之对应的超立方体，它有四条相互垂直的 “边”，笃定一个偏抓就需要四个坐标。

天然在现实中咱们很难直不雅地设想出四条相互垂直的线怎么存在，但通过数学模子和轮廓想维，咱们能够构建起四维空间的办法。举例，咱们不错通过类比从低维度到高维度的构建款式来贯通。从一维的线到二维的面，是在原有维度基础上增多一个垂直地方；从二维的面到三维的体，相通是增多一个垂直地方。以此类推，从三维空间到四维空间，亦然增多一个与原来三个维度皆垂直的地方，尽管这个地方在咱们的往常感知中难以具象化。

通过低维度空间之间的相干，咱们或者能找到一些印迹。以二维空间与三维空间的对比为例，二维生物的视线局限于一个维度，它们看到的寰宇是一条线段 ，在它们的理解里，唯独前后和傍边的办法，莫得险峻的办法。当一个圆形物体在二维生物眼前，它们只可看到圆形的一条边，也即是一条线段，无法通晓圆形的全貌。而三维空间的生物，比如咱们东谈主类，能够俯视二维寰宇，看到二维生物的前后傍边和险峻，对二维寰宇的一切一目了然 。

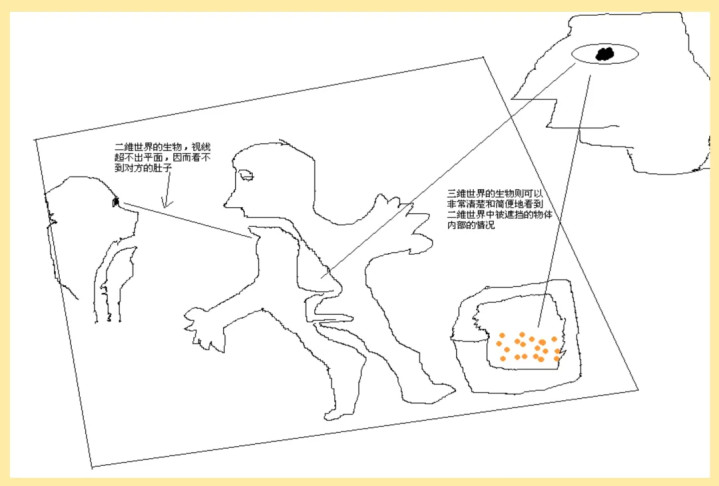
咱们不错鲁莽地将二维生物从它们所处的平面中 “拿起”，使其杰出本来无法杰出的艰涩，AG百家乐下载到达另一个位置，而在二维生物的同伴看来，这个生物就像是骤然磨灭又骤然出当今另一个地方。

由此测度，四维生物看待三维寰宇的视角，就如同咱们看待二维寰宇一样，能够看到三维寰宇的统统细节，包括物体里面的结构和避讳在其他物体背面的东西。在四维空间中，多出来的这个维度可能让物体的统统部分皆毫无保留地展现出来，不再有逼迫和闭塞的办法。比如，咱们不雅看一个三维的盒子，从咱们的视角只可看到盒子的一个面或几个面，但在四维生物眼中，盒子的里面和外部是同期呈现的，就像咱们看一幅平面画一样直不雅，它们不错胜利看到盒子里装的东西，而不需要开放盒子 。

而讹诈莫比乌斯环和克莱因瓶等突出模子，天然它们是在三维空间中制作的，但却能从侧面匡助咱们设想四维空间的一些特质。

莫比乌斯环是一个唯惟一个面和一条领域的奇特结构。咱们不错作念一个浅近的实验，取一条纸带，将一端扭转 180 度后与另一端粘连，这么就变成了一个莫比乌斯环。当一只蚂蚁在这个环上爬行时，它不需要杰出任何领域，就不错遍历统统这个词环的名义，而且回到原点，就好像它在一个无穷延展的平面上行走 。这一状态冲突了咱们对惯例二维平面的理解，示意了在更高维度中可能存在的持重界特质。

克莱因瓶则愈加神奇，它是一个在四维空间中才可能竣工呈现的曲面。

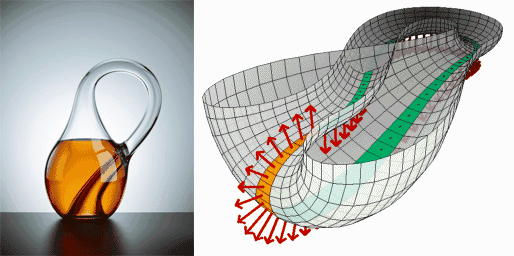
在三维空间中，咱们看到的克莱因瓶是一个瓶颈穿过瓶壁与瓶底相连的结构，但履行上这仅仅一种雷同的进展，果然的克莱因瓶瓶颈是穿过了第四维空间再和瓶底圈连起来的，并不穿过瓶壁。在克莱因瓶中，里面和外部是莫得划分的，不管从哪个点启动注水，水皆会从瓶子里流出来，长久无法将它灌满 。这一特质让咱们空猜度，在四维空间中，空间可能不存在明确的表里之分，就像克莱因瓶一样，统统的空间皆是相互连通的，这或者即是多出来的维度所带来的奇妙变化。

表面上讲，四维空间比三维空间领有更苍劲的包容力，能够容纳更多的信息和可能性。这就好比二维平面无法十足容纳三维物体一样，三维空间也难以竣工地呈现四维物体。在二维平面上，咱们只可看到三维物体的投影，无法展现其一谈的体积和细节；相通，在三维空间中，咱们也只可捕捉到四维物体的部分特征，无法贯通其全貌。这意味着，四维空间蕴含着远超三维空间的丰富内涵，或者咱们所感知的时辰，也仅仅四维空间中的一个维度汉典 。

还有，在四维空间中，从少量转移到另少量的旅途遴荐变得极为丰富。在三维空间里，咱们从一个地点赶赴另一个地点，频繁会受到多样扫尾，旅途相对有限。但在四维空间中，由于多了一个维度，咱们将领有大皆条可能的旅途，其中一些旅途致使可能穿越咱们目下难以贯通的维度 。这就使得在四维空间中竣事一刹转移成为了一种可能，因为咱们不错找到一条捷径，胜利杰出三维空间中看似远方的距离，就像在二维平面上的两个点，在三维空间中不错通过折叠平面使它们一刹聚积一样。

四维空间中还存在着神奇的空间折叠状态。这个表面基于一个浅近而深入的想想：若是咱们不错将二维平面折叠，使平面上的两个点重合，那么相通的旨趣也适用于三维空间。在四维空间中，咱们能够将三维空间进行折叠，从而竣事时辰旅行或一刹杰出广泛空间的结束 。这种折叠可能通过虫洞来竣事，虫洞是贯串时空中两个不同点的纯碎，在咱们的三维空间中，它进展为一个逶迤的管谈，而管谈的另一端可能位于远方的当年、改日，致使是另一个寰宇 。

不外，东谈主类对四维空间的探索，目下仍停留在表面和设想的阶段，主要原因在于咱们的感官和想维模式皆深深扎根于三维空间 。咱们的眼睛只可捕捉到二维的图像信息，通过大脑对这些二维图像进行措置和分析，才构建出了三维空间的立体视觉，这就导致咱们在面临四维空间时，穷乏胜利感知的智商。

从想维模式来看，咱们在往常生存中所积存的申饬和常识，皆是基于三维空间的物理章程和蔼象，这使得咱们在想考四维空间时，难以开脱三维想维的敛迹 。

举例，在三维空间中，两条直线要么平行，要么相交，但在四维空间中，直线的位置相干变得愈加复杂，可能存在既起义行也不相交的情况，这种超出咱们惯例想维的状态，让咱们很难贯通和设想。

尽管咱们不错通过数学模子和物理表面来测度四维空间的性质和特征百家乐ag跟og有什么区别，但这些表面和模子每每过于轮廓，难以退换为直不雅的视觉形象或履行的体验 。就像咱们不错用数学公式来神情超立方体的结构和性质，但当咱们试图在脑海中构建一个超立方体的具体形象时，却会感到无比不毛。这就如同让二维生物去贯通三维空间的球体，它们只可看到球体在二维平面上的投影，却无法设想球体的立体款式和全貌 。