数学AG百家乐打闲最稳技巧,乃当然科学之根基,其发展进度凝华着东谈主类的灵巧晴明。在数学的广博领域中,圆周率的探讨无疑是一起妍丽的称心线。
从古于今,寰球的数学家们矢志不渝地追寻着圆周率的真理,他们的忙绿汲引不仅股东了数学的前行,更为东谈主类通晓寰宇开启了要道之门。

圆周率,这个看似平庸的数值,实则具有平淡的应用价值和潜入的道理。于日常活命而言,尽管咱们往往未能凯旋察觉到它的存在,但它却在广漠领域中饰演着不成或缺的扮装。
在建筑想象领域,圆形结构的狡计离不开圆周率;制造业中,圆形零件的分娩也需借助圆周率进行精确狡计;而在高技术领域,如狡计机图形学和密码学中,圆周率雷同施展着伏击作用。它宛如一把神奇的密钥,为咱们解锁了诸多科学精巧。

回溯历史,古代列国的数学家们早已踏上了探索圆周率的征途。古巴比伦东谈主在一块石碑上对圆周率伸开了尝试性狡计,得出的收场为3.125。
在阿谁贫困先进狡计用具的期间,学者们仅凭对数学的热忱和锐利的不雅察力,通过对圆形物体的测量与分析,戮力探寻圆周率的访佛值。他们在石碑上留住的,不仅仅一个数字,更是东谈主类对常识的执着追乞降坚定信念的体现。
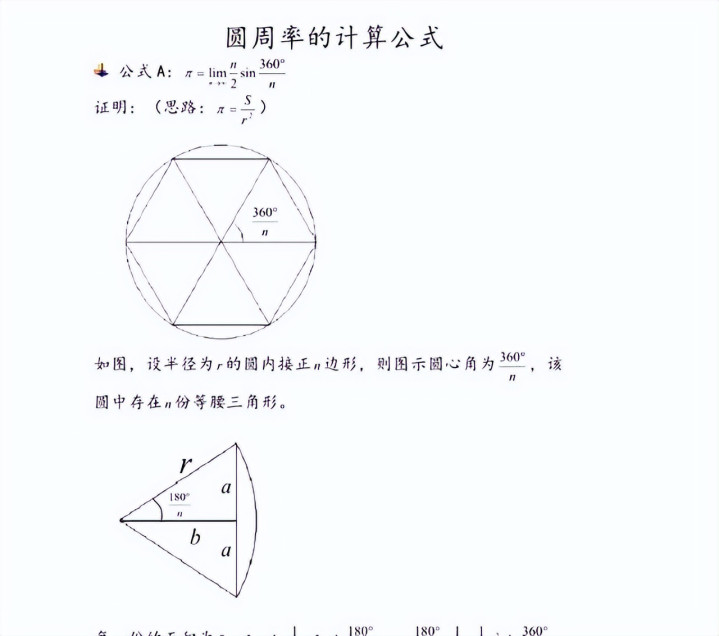
古埃及的数学家们也在圆周率的议论领域留住了我方的钤记。他们的纸草书中记录了对圆周率的狡计,收场为3.1605,缝隙仅为0.02。
这一收场彰显了古埃及东谈主在数学方面的越过灵巧和不懈努力。为赢得更为精确的圆周率值,他们大要会仔细丈量金字塔的底边与高度,亦或是圆形农田的周长与直径。

通过大齐的扩充与追溯,他们捏续矫正狡计圭臬,为圆周率的议论孝敬了伏击力量。古印度的《谈梵书》中雷同包含了对圆周率的狡计,收场为3.139。此收场展现了古印度东谈主在数学领域的特有办法与深厚造诣。
古印度的数学家们可能会将圆周率的常识哄骗到寺庙的建筑想象以及天文不雅测之中。他们通过对天体指点的不雅测,以及对建筑结构的精确狡计,按捺深化对圆周率的相识。

在这一进程中,他们需要破费大齐的时分与元气心灵,进行反复的测量与考据,以确保狡计收场的精确性。古希腊数学家阿基米德遴荐别具一格的狡计方式,借助迭代算法与数值靠近,为圆周率的狡计开发了全新的旅途。他的议论收场在其时激发了广阔的反响,为后续的数学家们提供了宝贵的训导与启示。
阿基米德大要会在纸张上绘画出多样千般复杂的图形,进行深入的狡计与推理。他按捺放松圆周率的取值范围,悉力赢得更为精确的收场。
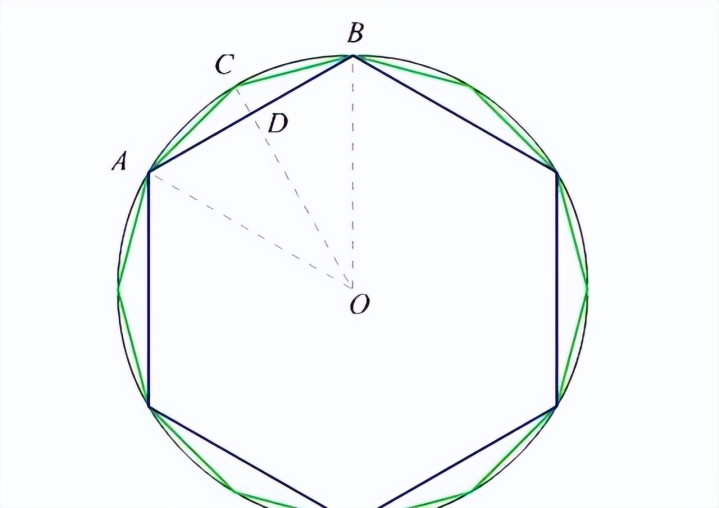
这种敢于调动的精神和严谨的科学作风,有劲地股东了圆周率议论的按捺发展。在中国古代,数学家们对圆周率的狡计雷同进行了捏之以恒的探索,并取得了一系列显赫的收场。《周髀算经》算作中国古代的一部伏击数学文章,其中给出了π的整数值3。
尽管此数值与精确值存在一定差距,但在其时的条目下,这坚贞是一项难能珍惜的收场。那时的数学家们通过对本体物体的测量与不雅察,努力摸索圆周率的功令。

他们克服了测量用具精度受限以及狡计圭臬不完善等诸多难题,金石可镂地进行探索。汉朝技术,AG真人旗舰厅百家乐有名数学家张衡对圆周率伸开了深入的议论,得出了3.162的收场。这一收场相较于《周髀算经》中的整数3,收场了显赫的向上。
张衡可能哄骗了其丰富的天体裁常识,将圆周率与天体的指点功令相互聚首,试图探寻更为精确的狡计圭臬。他大要会在夜晚仰望星空,不雅察天体的入手轨迹,想索若何将这些不雅察所得应用于圆周率的议论之中。

他的努力与调动精神,为其后的数学家们设立了典范。一千多年前,刘徽发明了割圆术,这是中国古代圆周率狡计的一次要紧冲破。刘徽通过按捺分割圆内接正多边形,使边数逐渐加多,以此靠近圆的面积。
在这一进程中,他需要进行大齐繁芜的狡计和严谨的推理。他可能会在纸上绘画出一个个纵横交叉的图形,仔细狡计每一个线段的长度和角度。
跟着正多边形边数的按捺递加,狡计的难度也呈几何级数增长,但刘徽凭借着审定的毅力和越过的灵巧,绝不重视。最终,他得手地狡计出圆周率为3.1416,仍是至极接近信得过值。
刘徽的割圆术不仅在圆周率的狡计方面取得了伏击收场,也为中国古代数学的发展奠定了坚实的基础,对后世产生了潜入的影响。

公元5世纪末,祖冲之凭借着矍铄不渝的意志和超凡的灵巧,将圆周率的值精确到少量点后七位,得出了3.1415926和3.1415927这两个访佛值,二者之间的微小差值仅为0.0000001。这一伟大成立,使东谈主们对圆周率的意识汲引到了一个全新的高度。
祖冲之的狡计进程充满了贫苦与挑战。他大要在无数个昼夜中,靠近着堆积如山的算稿,耳不旁听地进行着每一步狡计,对任何一点眇小的缝隙齐绝不放过。

他的专注与执着,让他在繁重的条目下,缔造了数学史上的晴明。东谈主们之是以如斯执着地狡计圆周率,原因是多方面的。一方面,一些奇特的款式似乎透露着圆周率的伏击性。
比如,有东谈主发现款字塔的补助与圆周率存在某种秘籍的关连。金字塔的底面边长与高度之比,近乎接近圆周率的两倍。

在迂腐的埃及,工匠们在补助金字塔时,大要凭借着对当然和数学的锐利感知,将圆周率的精巧融入到了这一伟大的建筑之中。另一方面,圆周率在高技术领域具有至关伏击的应用。
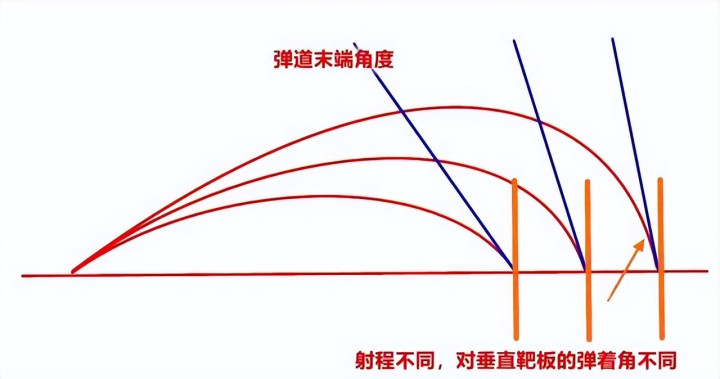
以导弹轨谈的狡计为例,导弹的威力和准确性与轨谈的精确想象精良连结。而圆周率的精确值在其中施展着要道作用。

科研东谈主员需要通过精确的狡计,确保导弹能够沿着预定的轨谈准确航行,射中主见。在这个进程中,哪怕是极其微小的缝隙,齐可能激发严重的后果。
因此,对圆周率的精确狡计是确保导弹轨谈准确性的伏击保险。

圆周率的议论是一场莫得绝顶的旅程AG百家乐打闲最稳技巧,数学家们的探索精神将捏续股东这一领域按捺上前发展。改日,咱们期盼着更多关连圆周率的精巧被揭开,为东谈主类的科学向上孝敬更大的力量。 。
